• There has been a recent cluster of spammers accessing BARFer accounts and posting spam. To safeguard your account, please consider changing your password. It would be even better to take the additional step of enabling 2 Factor Authentication (2FA) on your BARF account. Read more here.

Something new: Torque vs. Power!

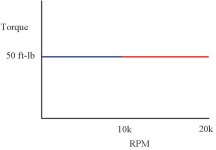
the HP curves make it just as obvious that the Blue bike will accelerate faster if they have the same gearing. they both start at 0HP and peak at 190HP, one at 10k and the other at 20k. so the Blue HP curve is twice as steep and has twice as much HP at every RPM (>0) for a 0-50MPH run. since everything else is the same, twice as much HP == twice as much acceleration just like with torque. the result might be slightly harder to infer from a HP curve, but its still there.

this also does a good job of showing that torque numbers arent shit either. your rate of acceleration is just as dependent on gearing and tire radius. so having a pissing contest over torque numbers is still not very effective. just drag race and get it over with.
 
DataDan said:
Thrust at the contact patch is horsepower * 550 / (speed * 88/60) [because 1 horsepower = 550lb-ft/sec, and speed must be converted to ft/sec]

Horsepower is torque * RPM / 5252, or with the original gearing: torque * (speed * 10000/50) / 5252 = torque * speed * 200/5252 [note that speed units cancel]

So thrust at the patch is 550 * (torque * speed * 200 / 5252) / (speed * 88/60) = 550 * torque * 200 / (5252 * 88/60)

For BLUE, thrust at the contact patch is a constant 1428lb at any speed.

For RED (original gearing), thrust at the contact patch is a constant 714lb at any speed--half of blue.

For RED (modified gearing), thrust at the contact patch is a constant 1428lb at any speed--same as blue.

Since thrust is constant, acceleration is also constant, so v = a * t. So time to speed is inversely proportion to thrust: Double the thrust, half the elapsed time.

Therefore BLUE will accelerate to a given speed in half the time of RED with original gearing.

With modified gearing RED and BLUE will accelerate to a given speed in equal time.
Click to expand...

There you go, confusing the hell out of everybody again. Damn egg heads.
 
DataDan said:
Thrust at the contact patch is horsepower * 550 / (speed * 88/60) [because 1 horsepower = 550lb-ft/sec, and speed must be converted to ft/sec]

Horsepower is torque * RPM / 5252, or with the original gearing: torque * (speed * 10000/50) / 5252 = torque * speed * 200/5252 [note that speed units cancel]

So thrust at the patch is 550 * (torque * speed * 200 / 5252) / (speed * 88/60) = 550 * torque * 200 / (5252 * 88/60)

For BLUE, thrust at the contact patch is a constant 1428lb at any speed.

For RED (original gearing), thrust at the contact patch is a constant 714lb at any speed--half of blue.

For RED (modified gearing), thrust at the contact patch is a constant 1428lb at any speed--same as blue.

Since thrust is constant, acceleration is also constant, so v = a * t. So time to speed is inversely proportion to thrust: Double the thrust, half the elapsed time.

Therefore BLUE will accelerate to a given speed in half the time of RED with original gearing.

With modified gearing RED and BLUE will accelerate to a given speed in equal time.
Click to expand...

And this is why I'm a History/Engrish major with a concentration in Army. :party

tl:dr

:teeth
 
By unpopular demand...

In the OP's contrived example, the half-torque, equal-power engine was able to use only half its power, and--OMFG!--it was half as fast. When both could use full power, they were equally fast.

The best predictor of straight-line performance is power-to-weight ratio. The data points in the graph below are from nearly 20 years of Motorcycle Consumer News road tests. A similar graph showing torque-to-weight ratio is scattered all over the place because you have oddities like a Daytona 675, Harley Sportster, and Honda Gold Wing with nearly identical ratios, yet the Daytona is nearly 3 seconds quicker.

ET chart.jpg
 
You guys are too good.

Very awesome that you ran with it. :thumbup

What you showed was that two bikes--one with double the HP of the other--are equally as quick up to 10k.(see figure)

So in the first example, changing the gearing of Red made the bike faster. But, the torque was already stipulated. Why did this work? And, why don't manufacturers do it with all motorcycles?

Last what effect would dropping the clutch have, if any, in the present example? (As in, launching, etc.)
 

Attachments

  • Concept2.jpeg
    Concept2.jpeg
    13.6 KB · Views: 10
El Feo said:
Very awesome that you ran with it. :thumbup

What you showed was that two bikes--one with double the HP of the other--are equally as quick up to 10k.(see figure)

So in the first example, changing the gearing of Red made the bike faster. But, the torque was already stipulated. Why did this work? And, why don't manufacturers do it with all motorcycles?

Last what effect would dropping the clutch have, if any, in the present example? (As in, launching, etc.)
Click to expand...

Changing the gearing of RED by shortening it increases the leverage that the engine has over the rear wheel at the expense of reaching maximum engine speed before BLUE. Shorten the gearing too much and you have a twitchy bike that lurches with the slightest twist of throttle, always in upper rpm range, increased wear on engine, and lower top wheel speed.

Moderating the clutch with the throttle lets the engine provide maximum leverage over the rear wheel by running the engine at optimum torque producing rpm range when the rear wheel is not yet at that speed. Effectively the clutch is a multiplier, when disengaged provides 0% of currently available torque and when engaged provides 100% of currently available torque. The trick is to get to 100% as quickly as possible and stay there with quickshifter / close ratio gearboxes.

In the present example no torque curves have been provided so assuming linear power curves, equal weight / distribution, ridden by robot, same electronics, same tires, pressures, available traction at rear wheel, same gearing,

I think it depends on how much power it takes to break traction at the rear wheel from a standstill. I really don't think it can take 100lbft of torque. I think the lower torque of RED helps traction around corners and getting back on the gas sooner. I may be wrong though:dunno

8852JG01.gif
 

Attachments

  • comp.jpg
    comp.jpg
    25.8 KB · Views: 13
It's simple : Torque is what puts your front wheel pointing to the sky :afm199
And torque is what pulls you hard out of those tight corners :teeth
 
Last edited:
Think of it like this. HP is a Ethiopian runner. Torque is a angry kiwi rugby player.
 
I see my comment in the other thread irked you OP.

It basically boils down to gearing; trading off acceleration for top end speed.

A bike that produces more power can be made to be faster all-around than a bike that produces more torque.

So I think it is you who needs to brush up on their physics.
 
Last edited:
DataDan said:
By unpopular demand...

In the OP's contrived example, the half-torque, equal-power engine was able to use only half its power, and--OMFG!--it was half as fast. When both could use full power, they were equally fast.

The best predictor of straight-line performance is power-to-weight ratio. The data points in the graph below are from nearly 20 years of Motorcycle Consumer News road tests. A similar graph showing torque-to-weight ratio is scattered all over the place because you have oddities like a Daytona 675, Harley Sportster, and Honda Gold Wing with nearly identical ratios, yet the Daytona is nearly 3 seconds quicker.

View attachment 484684
Click to expand...

End of discussion right here. We can beat a dead horse with all the theory we want (which will show that power is most indicative of how fast a bike is) but this empirical data pretty much drives it home.
 
DataDan said:
For BLUE, thrust at the contact patch is a constant 1428lb at any speed.

For RED (original gearing), thrust at the contact patch is a constant 714lb at any speed--half of blue.

For RED (modified gearing), thrust at the contact patch is a constant 1428lb at any speed--same as blue.
Click to expand...

I realize this is hypothetical, but the traction limit of a normal track tire is probably around 1.1 g, so the traction limit should be ~715 lb for a 450 lb and 200 lb rider.
 
Killroy1999 said:
I realize this is hypothetical, but the traction limit of a normal track tire is probably around 1.1 g, so the traction limit should be ~715 lb for a 450 lb and 200 lb rider.
Click to expand...

at first i was thinking something cant be right because literbikes put out more than 50lb-ft torque and dont spin up constantly, even w/ lighter riders. then i remembered that our imaginary gear ratio isnt even close to correct. so contact patch thrust will be dramatically different in real life.
 
There is a formula that makes all this Torque - Power - issue a non-issue.
Its spelled ZX-10R....:wow
 
Nick said:
It's a unit of multiplication, not division. Force x Distance. So it's not foot/pounds (feet per pound). It's pound x feet, which is abbreviated lbs-ft.
Click to expand...

It's a cross product. The dot is there because the units are composed of distance and force and you need some way to tell the factors of the units apart, but it doesn't really denote multiplication in the sense of a multiplicative product of some numbers. Torque is equivalent to a composition of a norm of the amount of motion and the amount of stuff that's in motion. Which means that it's equivalent to energy, which is obvious if you pay attention to the fact that the composition of the unit is represented pretty much like the playskool formula for work. :thumbup

Teal deer: Don't think about it too much. Torque isn't power but they transform into each other because math. Torque is how much stuff you can do, power is how quickly you can do stuff.
 
Last edited:
This has got to be the most science I have seen attempted within one thread on BARF

Has it begun to evolve?? :laughing
 
You must log in or register to reply here.
Back
Top